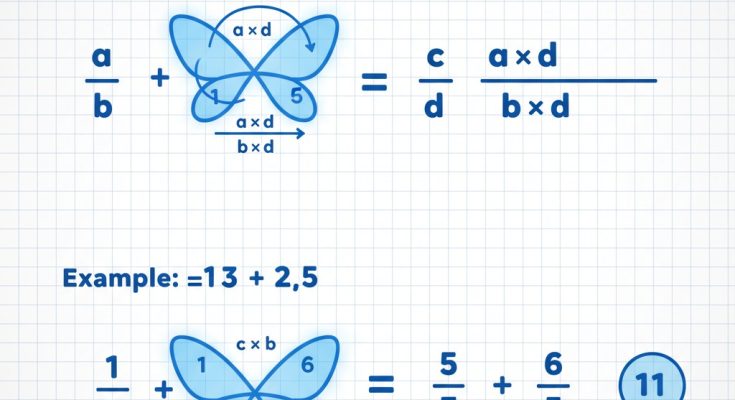Conquering Fractions: Your Fast Track to Addition and Subtraction!

Fractions – they can seem daunting, a jumble of numbers stacked on top of each other. But what if I told you that adding and subtracting them doesn’t have to be a slow, agonizing process? Forget the fraction phobia, because today we’re unlocking some quick and easy methods to tackle these operations like a pro!

Before we dive into the speedy techniques, let’s remember the golden rule of fraction addition and subtraction: You can only add or subtract fractions that have the same denominator. If they don’t, your first step is always to find a common denominator. Think of it like trying to add apples and oranges – you need a common unit (like “fruit”) before you can combine them!

Method 1: The “Butterfly” or “Cross-Multiplication” Method (for two fractions)

This method is a fantastic shortcut when you’re dealing with just two fractions. It’s visual, intuitive, and often bypasses the need to explicitly find the Least Common Denominator (LCD) right away.

Let’s say you want to add

 $ab+cd\frac{a}{b} + \frac{c}{d}$

Multiply diagonally, like a butterfly’s wings!
- Multiply
```
 $a$ 
```
  by
```
 $d$ 
```
  .
- Multiply
```
 $b$ 
```
  by
```
 $c$ 
```
  .
- These become your new numerators.
Multiply the denominators together. This will be your new common denominator.
Combine! Add (or subtract) your new numerators over the new common denominator.

Example: Let’s add

 $13+25\frac{1}{3} + \frac{2}{5}$

Multiply
```
 $\times 5 = 5$ 
```
Multiply
```
 $\times 2 = 6$ 
```
Multiply
```
 $\times 5 = 15$ 
```
(our common denominator)

So,

 $13+25=515+615=5+615=1115\frac{1}{3} + \frac{2}{5} = \frac{5}{15} + \frac{6}{15} = \frac{5+6}{15} = \frac{11}{15}$

Voila! It’s like magic!

Method 2: Finding the Least Common Multiple (LCM) – The Efficient Denominator

While the butterfly method is great for two fractions, when you have more than two, or when the denominators share common factors, finding the Least Common Multiple (LCM) is often the most efficient route to a common denominator.

The LCM is the smallest number that is a multiple of all your denominators. Using the LCM keeps your numbers smaller and your calculations simpler.

How to find the LCM quickly:

List multiples: Start listing multiples of the largest denominator until you find a number that is also a multiple of the other denominators.
- Example: For
```
 $4 1 + 6 1$ 
```
  , the largest denominator is 6.
  - Multiples of 6: 6, 12, 18…
  - Is 6 a multiple of 4? No.
  - Is 12 a multiple of 4? Yes! So, 12 is your LCM.
Prime Factorization: For larger or more complex denominators, break each denominator down into its prime factors. The LCM will be the product of the highest power of each prime factor present in any of the denominators.
- Example: For
```
 $12 1 + 18 1$ 
```
  - ```
   $12 = 2^{2} \times 3$ 
```
- ```
 $18 = 2 \times 3^{2}$ 
```
  - LCM =
```
 $2^{2} \times 3^{2} = 4 \times 9 = 36$ 
```

Once you have your LCM:

Convert each fraction: For each fraction, figure out what you multiplied the original denominator by to get the LCM. Then, multiply the numerator by that same number.
Add/Subtract: Now that all your fractions have the same (LCM) denominator, simply add or subtract the numerators and keep the denominator the same.

Example: Let’s subtract

 $6 5 - 8 3$

Find the LCM of 6 and 8.
- Multiples of 8: 8, 16, 24…
- Is 24 a multiple of 6? Yes! LCM = 24.
Convert fractions:
- ```
 $6 5$ 
```
  : To get 24, we multiplied 6 by 4. So, multiply 5 by 4:
```
 $6 \times 4 5 \times 4 = 24 20$ 
```
- ```
 $8 3$ 
```
  : To get 24, we multiplied 8 by 3. So, multiply 3 by 3:
```
 $8 \times 3 3 \times 3 = 24 9$ 
```

Subtract:

 $24 20 - 24 9 = 24 20 - 9 = 24 11$

Method 3: Dealing with Mixed Numbers

Don’t let mixed numbers (like

 $2 2 1$

) slow you down! There are two main approaches:

Convert to Improper Fractions: This is often the most straightforward method, especially for subtraction.
- Multiply the whole number by the denominator, then add the numerator. Keep the same denominator.
- Example:
```
 $2 2 1 = 2 ( 2 \times 2 ) + 1 = 2 5$ 
```
- Once converted, proceed with the methods above.
Add/Subtract Whole Numbers Separately (for addition):
- Add the whole numbers together.
- Then, add the fractional parts separately using one of the methods above.
- Example:
```
 $2 3 1 + 1 2 1$ 
```
  - Whole numbers:
```
 $2 + 1 = 3$ 
```
  - Fractions:
```
 $3 1 + 2 1$ 
```
    (using butterfly:
```
 $6 2 + 6 3 = 6 5$ 
```
    )
  - Combine:
```
 $3 + 6 5 = 3 6 5$ 
```
- Caution: This method can get tricky with subtraction if the first fraction is smaller than the second. In those cases, converting to improper fractions is safer.

Practice Makes Perfect!

The key to mastering these quick methods is practice. Grab a pen and paper (or a whiteboard!) and work through a few problems each day. You’ll be zipping through fraction problems in no time!

Do you have a favorite fraction-solving trick? Share it in the comments below!

Conquering Fractions: Your Fast Track to Addition and Subtraction!